MI-Sim A MATLAB Package for the Numerical Analysis of Ecological Motifs

• Home
• Installation
• Getting Started
• Documentation
• Glossary
• Thermodynamics module
• GUI Interface
• Examples
• Algorithms

Contents

• Screenshot
• Description
• Stoichiometry
• References

Screenshot

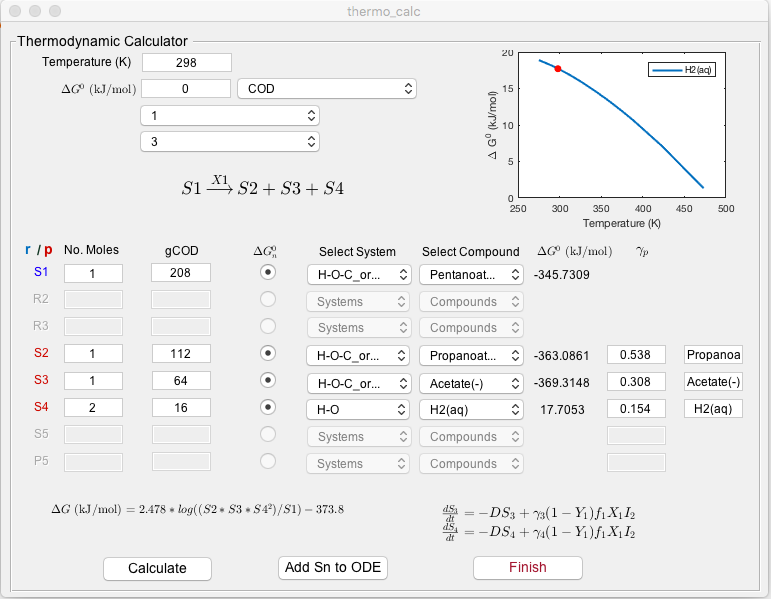
Description

This module is available upon selection of the thermodynamics growth model from the MI-Sim interface. At present, the thermodynamics is modelled only for the inhibition function, $I_2$, applicable to the cooperation/syntrophy and three-species motifs. The growth model functions, $f_n$, default to Monod form in all cases. Furthermore, thermodynamic inhibition only has meaning in microbial systems and should not be used for interactions at higher trophic scales.

The thermodynamic calculator comprises three steps:

• System specification: The user should enter the operating temperature (K), reaction $\Delta G^0$ (kJ/mol), and the index of reactants ($r$) and products ($p$) in the reaction. $\Delta G^0$ can be set to zero if the user wishes to automatically calculate the $\Delta G$ value for each component of the reaction from the drop-down menus. For compounds not available in these menus, the cumulative $\Delta G$ values must be entered in the $\Delta G^0$ box provided. Although $r$ and $p$ are set to one in all motif reactions, it is necessary here to specify the actual reaction stoichiometry to properly define its thermodynamics. Hence, there may be more reactants or products involved that are not explicitly modelled by MI-Sim. A simple text display of the reaction is provided to indicate the substrates, $S_n’$ and biomass $X_n$ involved in the conversion.

• Compound specification: In the central block of the calculator, the user may input stoichiometric information for each reactant and product featured in the reaction. This includes the number of moles of substrate product, the molar mass of each compound (g/mol) and, if required, the option to calculate the Gibbs Free Energy for each compound. For the latter, the user must specify the compound using drop-down menus to choose the chemical system where it is found, and its state (e.g., solid, liquid, aqueous, gas). For the product compounds, the user must specify their stoichiometric coefficient, $\gamma_p$, which is described in the Stoichiometry section.

• Calculation: The calculation of the thermodynamic inhibition function is executed by pressing the Calculate button. The functions described here are computed using the values provided by the user:

  $$I_2 = f(T,\Delta G,S_\nu,S_\pi)$$

  where $S_\nu$ are the reactants and $S_\pi$ the products, and $S_n’=(S_\nu,S_\pi)$. The values for the compound specific $\Delta G_n^0$ at temperature $T$ are taken from the $\Delta G^0$ tables at saturation pressure provided in Amend and Shock (2001). Polynomial curve fitting of order 2 is used to determine the $\Delta G^0$ values for the user-specified temperature, based on the temperature dependent curves developed from the values in the tables cited. The substrate concentrations are converted from moles to units COD.

  The Add Sn to ODE function automatically defines equations for the additional substrates ($S_{\nu,new}$ and $S_{\pi,new}$) not included in the selected motif. In the case additional reactants are included, a reconfiguration of the growth function for biomass $X_n$ is required to account for its growth on this additional substrate. The generic form of the additional equations are as follows:

  $$\frac{dS_{\nu,new}}{dt}=-DS_{\nu,new}-f_{new}X_nI_2$$ $$\frac{dX_n}{dt}=-DX_n+Y_{new}f_{new}X_nI_2-k_{dec,n}X_n$$ $$\frac{dS_{\pi,new}}{dt}=-DS_{\pi,new}+\gamma_{new}(1-Y_n)f_nX_nI_2$$ $$f_{new}=f_n\frac{S_{\nu,new}}{K_{S,new}+S_{\nu,new}}$$

  The Finish button closes the thermodynamic calculator module and returns the user to the main GUI interface.

Stoichiometry

To correctly apply thermodynamic principles, it is necessary to know the complete stoichiometry of the reaction. MI-Sim assumes that the ecological interactions involve only the conversion of a single reactant to a single product, which is often a satisfactory assumption when considering that secondary products play no role in the behaviour of the interaction. This, of course is not true for real-world environments, especially microbial systems that feature multiple functional groups of organisms with access to more than one energy source. Here, we can still apply thermodynamic principles within the constrained framework, but it is necessary to derive the full reaction stoichiometry in order to derive the true energy balance in the system.

In order to implement thermodynamics in the existing models, it is necessary to provide information about the reaction chemistry to then be able to calculate the inhibition function. The calculator is developed to work in units of Chemical Oxygen Demand (COD) and this must be calculated for each reaction substrate. It is then fairly straightforward to calculate the conversion coefficient explaining the fraction of each product converted from the reactant.

Example

To demonstrate the steps required to calculate the COD and $\gamma$ values required by the thermodynamic calculator, we present an example here in the case of anaerobic degradation of valerate ($S_1$) to propionate ($S_2$) and acetate ($S_3$) by organism ($X_1$). The assumption of acetate inhibition is made here, although this is not relevant to the calculations described.

The degradation reaction is given as:

$$\mathrm{C_5H_{10}O_2 + 2H_2O \rightarrow C_2H_4O_2 + C_3H_6O_2 + 2H_2}$$

Chemical Oxygen Demand calculations

First, we calculate the theoretical Chemical Oxygen Demand (tCOD) of each compound in the reaction by determining the number of moles of oxygen required to oxidise the compound to carbon dioxide ($\mathrm{CO_2}$) and water ($\mathrm{H_2O}$). For organics, the calculation is made using the formula:

$$\mathrm{C_xH_yO_z+ 0.25(4x+y-2z)O_2 \rightarrow xCO_2 + \frac{y}{2}H_2O}$$

Knowing that the molar mass of oxygen is 32g, we can calculate the tCOD as $\mathrm{8(4x+y-2z)}$ gCOD.

Hence, for the compounds involved in the example reactions, the tCOD values are as follows:

Valerate: $\mathrm{C_5H_{10}O_2}$ 208 gCOD

Propionate: $\mathrm{C_3H_6O_2}$ 112 gCOD

Acetate: $\mathrm{C_2H_4O_2}$ 64 gCOD

Hydrogen: $\mathrm{H_2}$ 16 gCOD

Stoichiometric conversion fractions ($\gamma_p$)

The $\gamma_p$ values can be derived directly from the stoichiometry of the reaction as they are calculated as the fraction of COD from the reactant that is converted to the product. In this example we have the reactant valerate converted to three products, where the COD balance is $\mathrm{208 = 112 + 64 + (2\times16)}$ gCOD. Subsequently, we calculate the conversion fractions as:

Propionate: $\gamma_0 = \mathrm{\frac{112}{208}= 0.538}$

Acetate: $\gamma_3 = \mathrm{\frac{64}{208}= 0.308}$

Hydrogen: $\gamma_4 = \mathrm{\frac{32}{208}= 0.154}$

We denote $p$ for acetate and hydrogen as 3 and 4, respectively, as these are additional products not included in the original motif.

References

Amend, J.P. and Shock, E.L. (2001). Energetics of overall metabolic reactions of thermophilic and hyperthermophilic Archaea and Bacteria. FEMS Microbiol Rev., 25(2), 175-243.

Grosskopf, T. and Soyer, O.S. (2016). Microbial diversity arising from thermodynamic constraints. ISME J., In Press.